基于 Golang 实现环形分布式哈希表

声明

本文译自: Chord: Building a DHT (Distributed Hash Table) in Golang

什么是分布式哈希表？

分布式哈希表是分布式系统的一种类别，它将键值对数据以哈希表的形式储存在分布式系统中，系统中的任何节点都可以有效的检索键值。

分布式散列表（英语：distributed hash table，缩写DHT）是分布式计算系统中的一类，用来将一个关键值（key）的集合分散到所有在分布式系统中的节点，并且可以有效地将消息转送到唯一一个拥有查询者提供的关键值的节点（Peers）。这里的节点类似散列表中的存储位置。分布式散列表通常是为了拥有极大节点数量的系统，而且在系统的节点常常会加入或离开（例如网络断线）而设计的。在一个结构性的延展网络（overlay network）中，参加的节点需要与系统中一小部分的节点沟通，这也需要使用分布式散列表。分布式散列表可以用以创建更复杂的服务，例如分布式文件系统、点对点技术文件分享系统、合作的网页缓存、多播、任播、域名系统以及即时通信等。(维基百科)

每个节点都有维护各自键值映射的责任。

分布式哈希表

分布式哈希表的性质

分布式散列表一般强调以下特性：

  • 离散性：也就是去中心化，构成系统的节点没有任何中央式的协调机制。
  • 伸缩性：即使有成千上万个节点，系统仍然十分有效率。
  • 容错性：即时接地点不断的加入、离开或者停止工作，系统仍然十分可靠。

什么是一致性哈希？

普通的哈希算法，在分布式系统中如果某个节点断开或新增节点时，计算的哈希值很可能在节点中找不到，无法保证一致性，需要重新计算所有的键值映射，成本非常高。而一致性哈希就是想让每次节点变动导致重新计算映射的成本尽可能的低一些。在使用一致性哈希算法后，哈希表大小的改变平均只需要对 K/n 个关键字重新映射，其中 K 是关键字的数量，n 是槽位数量。

一致性哈希的性质

  • 平衡性：指哈希的结果均匀分散到各个缓冲区中去，避免出现热点。
  • 单调性：指添加节点后，原有的哈希结果要么不迁移，要么迁移到新的节点，不会迁移到旧的节点。
  • 分散性：尽量降低同一内容被映射到不同缓冲区中的概率。
  • 负载：尽量降低某个节点的负荷，避免同一缓冲区被不同的值映射。
  • 平滑性：指系统中节点数目的平滑改变应该和键值对象的平滑改变是一致的。

什么是 Chord 算法？

在计算机领域，Chord 是一个点对点分布式哈希表的协议和算法。是 P2P 中的四大算法之一（其他三个分别是 CAN、Pastry、Tapestry），Chord 只负责如何把给定的键分配给节点，以及节点如何定位负责该键的节点进而找到给定键的值。

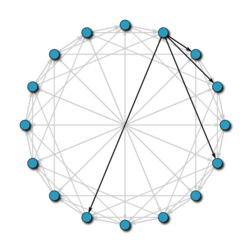
Chord

Chord 算法是基于一致性哈希的，更多信息可以参考 Ion Stoica，Robert Morris，David Karger，Frans Kaashoek 和 Hari Balakrishnan 的论文：original paper。

实现细节

1.基本查询

Chord 协议的核心用途就是从客户端（节点）查询一个 key。显然，任何查找只要沿着 Chord 环一圈肯定能找到，但是这会导致时间复杂度为 O(N), N 是环中的节点数。这对于一个上百万节点，且节点经常加入、退出的 P2P 网络来说是无法忍受的。为了避免上面的线性搜索，Chord 实现了一种更快的非线性搜索方法。这要求每个节点记录一张包含 m 条数据的 finger 表，因为 Chord 算法采用 SHA-1 作为哈希函数，SHA-1 会生成一个 2160 的空间，所以 finger 表的长度为 160。

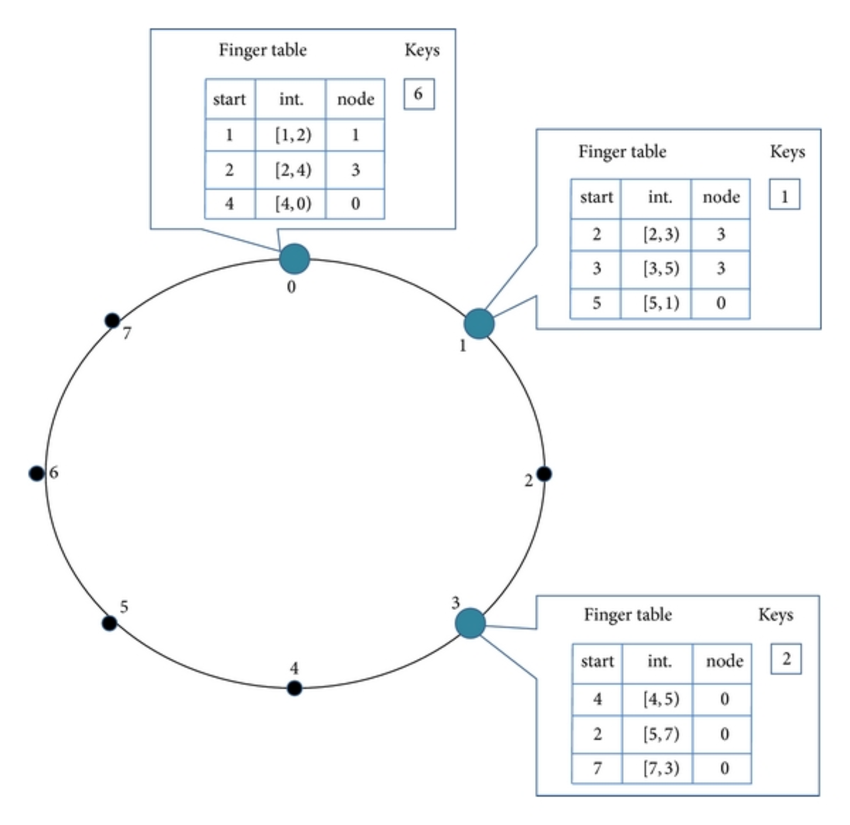
Chord-finger

该表的第 i 项值将存放节点 n的第 ((n+2i-1) mod 2m) 个后继节点（successor）。finger表的第一个条目实际上是节点的直接后继字段（因此不需要额外的后继字段）。每当一个节点想要查找一个键 k 时，它都会将查询传递给它 finger 表中最近的前继或后继节点（环中比ID比k小的最大值），直到一个节点发现 k 储存在它的直接后继节点中。这样的算法时间复杂度为 O(logN)。

// fingerEntry represents a single finger table entry
type fingerEntry struct {
   Id   []byte         // ID hash of (n + 2^i) mod (2^m)
   Node *internal.Node 
}

func newFingerTable(node *internal.Node, m int) fingerTable {
   ft := make([]*fingerEntry, m)
   for i := range ft {
    ft[i] = newFingerEntry(fingerID(node.Id, i, m), node)
   }
  return ft
}

// newFingerEntry returns an allocated new finger entry with the attributes set
func newFingerEntry(id []byte, node *internal.Node) *fingerEntry {
   return &fingerEntry{
    Id:   id,
    Node: node,
   }
}

// Computes the offset by (n + 2^i) mod (2^m)
func fingerID(n []byte, i int, m int) []byte {
   // Convert the ID to a bigint
   idInt := (&big.Int{}).SetBytes(n)

   // Get the offset
   two := big.NewInt(2)
   offset := big.Int{}
   offset.Exp(two, big.NewInt(int64(i)), nil)

   // Sum
   sum := big.Int{}
   sum.Add(idInt, &offset)

   // Get the ceiling
   ceil := big.Int{}
   ceil.Exp(two, big.NewInt(int64(m)), nil)

   // Apply the mod
   idInt.Mod(&sum, &ceil)
   // Add together
   return idInt.Bytes()
}

2.新节点加入

每当有新节点加入时，都应该维护三个不变量（前两个确保正确性，后一个保证快速查询）：

  1. 每个节点的后继节点正确的指向其直接后继节点
  2. 每个 key 都存储在后续 k 中
  3. 每个节点的 finger 表应该是正确的

为了满足这些不变量，为每个节点维护一个前置字段。

type Node struct {
  *internal.Node
  predecessor *internal.Node
  successor *internal.Node
  fingerTable fingerTable
  storage Storage
  transport Transport
}

对于新加入的节点n，应该执行以下任务：

  1. 初始化节点n的前置表和finger表
  2. 通知其他节点更新其前置和finger表
  3. 新节点从其后继节点接管其负责的 key
func (n *Node) join(joinNode *internal.Node) error {

    // First check if node already present in the circle
    // Join this node to the same chord ring as parent
    var foo *internal.Node

    // Ask if our id already exists on the ring.
    if joinNode != nil {
        remoteNode, err := n.findSuccessorRPC(joinNode, n.Id)
        if err != nil {
            return err
        }
        if isEqual(remoteNode.Id, n.Id) {
            return ERR_NODE_EXISTS
        }
        foo = joinNode
    } else {
        foo = n.Node
    }

    succ, err := n.findSuccessorRPC(foo, n.Id)
    if err != nil {
        return err
    }
    n.succMtx.Lock()
    n.successor = succ
    n.succMtx.Unlock()
    return nil
}

N 的前继节点可以很容易的从 successor(n) 的前继（在前一个循环中）获得。对于 finger 表，有各种初始化方法。最简单的方法就是对所有 m 条目执行所有的后继节点查询。结果是 O(M/logN)。一个更好的方法是检查 finger 表中的 ith 条目对于 (i+1)th 条目是否仍然准确。这样时间复杂度为 O(log2N)。

3.稳定

为了确保正确的查找，所有后继指针都必须是最新的。因此需要运行一个稳定的后台进程更新 finger 表和后继指针。

其工作方式如下：

  • stabilize(): 为其前继 p 询问他的后继节点，并决定 p 是否应该作为 n的后继节点。
  • notify(): 通知 n 的后继节点它的存在，因此它可以将其前身更改为 n。
  • fix_fingers(): 更新 finger 表
  • check_predecessor(): 定期检查前继节点是否处于活动状态。
/*
    NewNode creates a new Chord node. Returns error if node already
    exists in the chord ring
*/
func NewNode(cnf *Config, joinNode *internal.Node) (*Node, error) {
    if err := cnf.Validate(); err != nil {
    	return nil, err
    }
    node := &Node{
    	Node:       new(internal.Node),
    	shutdownCh: make(chan struct{}),
    	cnf:        cnf,
    	storage:    NewMapStore(cnf.Hash),
    }

    var nID string
    if cnf.Id != "" {
    	nID = cnf.Id
    } else {
    	nID = cnf.Addr
    }
    id, err := node.hashKey(nID)
    if err != nil {
    	return nil, err
    }
    aInt := (&big.Int{}).SetBytes(id)

    fmt.Printf("new node id %d, \n", aInt)

    node.Node.Id = id
    node.Node.Addr = cnf.Addr

    // Populate finger table
    node.fingerTable = newFingerTable(node.Node, cnf.HashSize)

    // Start RPC server
    transport, err := NewGrpcTransport(cnf)
    if err != nil {
    	return nil, err
    }

    node.transport = transport

    internal.RegisterChordServer(transport.server, node)

    node.transport.Start()

    if err := node.join(joinNode); err != nil {
    	return nil, err
    }

    // Peridoically stabilize the node.
    go func() {
    	ticker := time.NewTicker(1 * time.Second)
    	for {
    		select {
    		case <-ticker.C:
    			node.stabilize()
    		case <-node.shutdownCh:
    			ticker.Stop()
    			return
    		}
    	}
    }()

    // Peridoically fix finger tables.
    go func() {
    	next := 0
    	ticker := time.NewTicker(100 * time.Millisecond)
    	for {
    		select {
    		case <-ticker.C:
    			next = node.fixFinger(next)
    		case <-node.shutdownCh:
    			ticker.Stop()
    			return
    		}
    	}
    }()

    // Peridoically checkes whether predecessor has failed.

    go func() {
    	ticker := time.NewTicker(10 * time.Second)
    	for {
    		select {
    		case <-ticker.C:
    			node.checkPredecessor()
    		case <-node.shutdownCh:
    			ticker.Stop()
    			return
    		}
    	}
    }()

    return node, nil
}

大部分的细节可以在论文中找到。这里有一个简单的 gif 来演示 DHT 的工作：

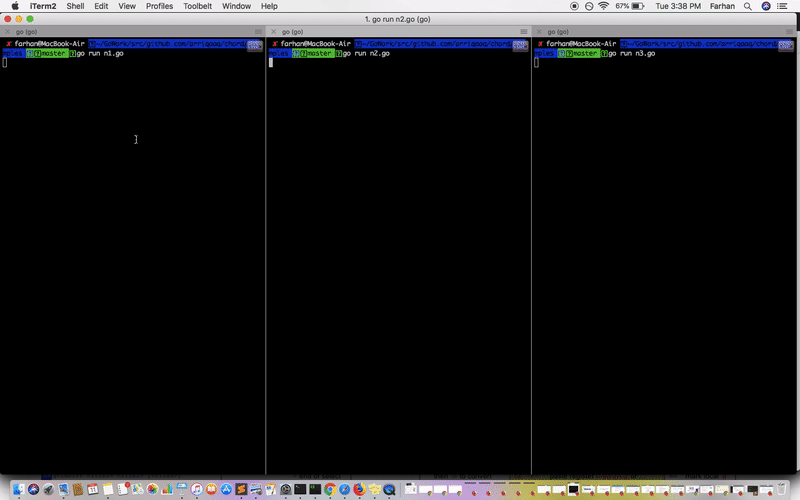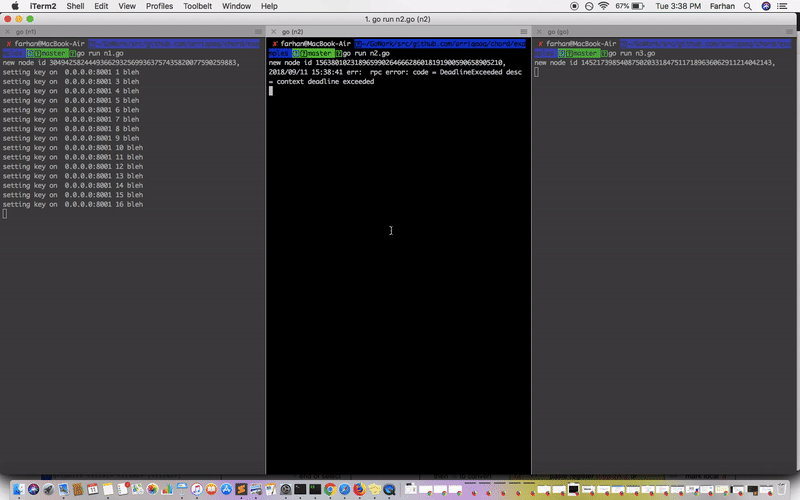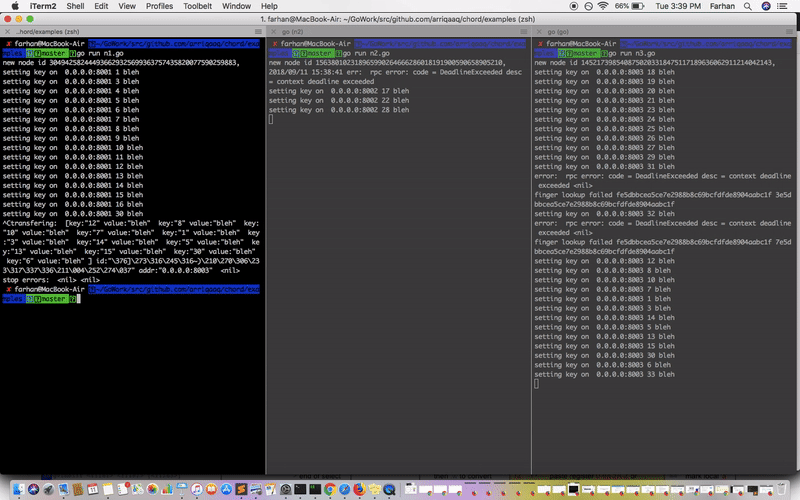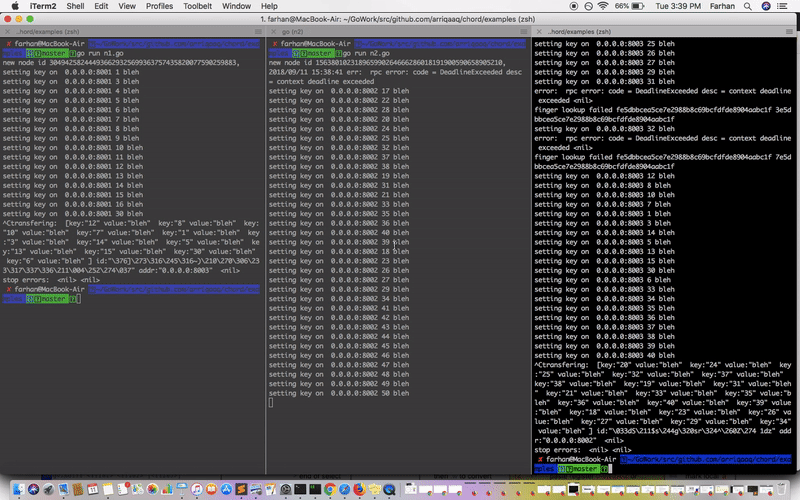
DHT-Work

当一个节点停机时，该节点的 key 将被转换至后继节点上。

以下为代码：

https://github.com/arriqaaq/chord

参考

  1. 从头到尾理解 Hash 表算法
  2. 五分钟看懂一致性哈希算法
  3. Chord 算法原理
  4. 一致性哈希和分布式哈希